1464
熵?这很容易!
这篇文章是在响应的意译是马克Eichenlaub 给了这个问题的什么是直观的方式来了解熵?,在网站上给出Quora的 i>的
熵。也许这是最困难的理解的概念,通过它可以在物理的过程中满足,至少当它涉及到经典物理学之一。几个研究生,可以解释它是什么。大多数问题与熵的理解,但是,可以删除,如果明白了一件事。熵是从其他热力学量有质的不同:如压力,体积,或内部的能量,因为它不是系统的属性,以及我们如何看待这个系统。不幸的是,在热力学过程中它通常与其他热力学函数,这加剧了误解考虑。
那么,什么是熵?
简而言之,该
<大段引用>熵 - 这是如何了大量的信息,你不知道系统 BLOCKQUOTE>例如,如果你问我,我住的地方,我会回答:在俄罗斯,我的熵值高的你,毕竟,俄罗斯大国。如果我给你打电话我邮政编码:603081,我的熵为你减少,因为你会得到更多的信息
。
邮编包含六个数字,那就是,我已经给你的信息,六个字符。熵你对我的知识下降约6个字符。 (事实上,这是不是因为有些指标对应多个地址,以及一些 - 少了,但我们忽略了这些)
。
或考虑另一个例子。假设我有十个骰子(十六进制),并把他们的,我告诉你,他们的总和等于30。只知道,你不能说每个骨头什么具体的数字 - 你没有足够的信息。在统计物理上的骨头,这些具体的数字称为微观,以及(在本例中30)的总金额 - 宏观态。有对应于这样的宏观态的熵是约6,5个字符(一半来自事实的量等于30 2930455微观即微观的顺序编号在第七排你,不是所有的数字,但只有0, 1和2)。
而且如果我告诉你,和等于59?要做到这一点,也只有10宏观态可能微观,使得它的熵是只有一个字符。正如你所看到的,不同的宏观态有不同的熵。
现在让我告诉你,第一个五年骨头13的总和,总和其余五 - 17,使超过30你有总量,但是,在这种情况下,提供更多的信息,因此系统对您的熵应该下降。事实上,5骨头13可以接收420个不同的方式,和17 - 780次,显微镜化妆即总数系统的唯一420h780 327 = 600。约一个字符的熵是比在第一实施例小。
我们测量记录微观的数目所需的字符数的熵。在数学上,它被定义为数目的对数,所以表示熵S中的符号,而微观符号Ω的数量,我们可以写出:
S =日志Ω
这不过是波尔兹曼式(最多一个因子k,取决于测量的选择的单位),进行熵。如果宏观态符合一项微观状态,它的熵这个公式是零。如果你有两个系统,总熵等于每个系统的熵的总和,因为日志(AB)=登录A +登录B.

从上面的描述可以清楚为什么我们不应该认为熵作为系统的性能。该系统具有opedelёnnye内部的能量,动量,充电,但它没有具体的熵:熵10骨头取决于你只知道他们的全部金额,或也部分和五岁以下儿童的骨骼
。
换句话说,熵 - 这就是我们如何描述系统。这使得它更从中取得物理学工作的其他值不同。
实物例证:在活塞
气 经典系统,这被认为在物理,是包含在所述活塞下的容器中的气体。气微状态 - 这是位置和它的每一个分子的动量(速度)。这等同于说你知道落在每个骨的早期上面的例子中的值。宏观态气体被描述这样的量如压力,密度,体积,化学组合物。这是关于轧制骰子的值的总和。
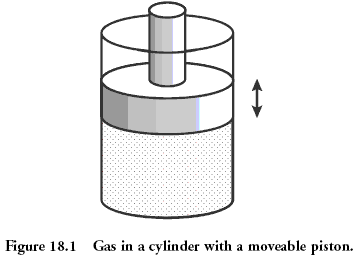
量描述宏观态可以通过一个所谓的“状态方程”可以相互结合。这种连接的存在允许,不知道微观预测会发生什么我们的系统,如果你启动加热或移动的活塞。对于状态的理想气体状态方程具有形式简单:
P =ρT
虽然你可能更熟悉的克拉珀龙 - 门捷列夫PV =νRT - 这是相同的公式,但与另外一对常量来迷惑你。更多的微状态满足这一宏观态是更多的粒子是我们的制度更好地描述其状态方程的一部分。为气体的颗粒数的典型值是阿伏伽德罗数,即10个顺序 23 SUP>的。
量,如压力,温度和密度平均的称呼,是因为它们的平均,对应于给定宏观态(或相当接近它的宏观状态)持续连续微观状态。要找出哪些微观状态是一个系统,我们需要大量的信息 - 我们需要知道每个粒子的位置和速度。这个信息的量称为熵。
如何在宏观态的熵的变化?这是很容易理解的。例如,如果我们有一个小的热气体,其颗粒将增加的速度,因此,将增加,并且我们的无知有关速度的程度,即,熵增。或者,如果我们增加气体的体积通过推动活塞以增加我们的粒子的位置的无知的程度,和熵也将增长。
固体和势能
如果我们考虑一个气体代替的固体本体,特别是与一个有序结构作为晶体,例如,一个金属片,其熵小。怎么会?因为知道在该结构中,要知道,和所有其他的位置(它们被布置成规则的晶体结构)的单个原子的位置,原子的速度是小的,因为它们不能飞离它们的位置和仅轻微振荡围绕平衡位置。< BR />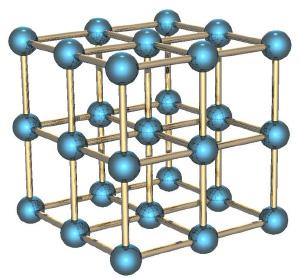
如果一块金属是在重力场中(例如,地球的表面上方升高),在该金属的每个原子的势能近似等于其它原子的势能,以及与此相关的能量熵是低的。这不同于动能势能,这对于热运动可以从原子向原子而变化。
如果一个金属片,提升到一定高度,让他们去,其势能转换成动能,而是熵增加会有一点,因为所有的原子会移动近似相同。但是,当一个片落在地上的击期间金属原子将具有随机的方向,和熵显着增加。的定向运动的动能进入热运动的动能。之前我们打了一些知道如何将每个原子,现在我们已经失去了这一信息。
了解热力学第二定律
热力学第二定律指出熵(封闭系统)总是增加。现在我们可以理解为什么:因为你不能一下子获得有关微观的更多信息。一旦你失去了关于微状态的一些信息(如影响地面上的一块金属的过程中),你不能返回回来。

让我们回到骰子。回想一下,一共有59宏观态具有非常低的熵,同时也得到它不是那么简单。如果一次又一次掷骰子,它会掉出的量(宏观态),其对应于更多数量的微观的是要实现宏观态大熵。最大熵共有35人,她就会更经常比别人落下。仅此而已,说热力学第二定律。任何随机(不受控制)相互作用导致的增加的熵的,至少直到它到达它的最大值。
搅拌气体
并保证说一个例子。假设我们有一个容器,其中有两个气体分离位于容器壁的中间。我们称一个气体分子蓝,其他 - 红
如果打开隔板,气体开始搅拌,因为微观的数,其中混合气体比微状态中它们被分离大得多,而且微状态所有天然同等。当我们打开该分区的每个分子,我们失去了分区的哪个方面的信息,这就是现在。如果分子是N,信息的N个位丢失(在这种情况下的位或符号,它实际上是相同的,并且仅相差一些常数因子)。
研究了麦克斯韦妖
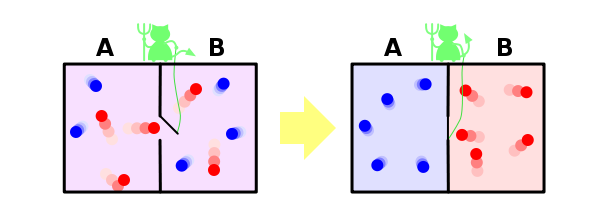
最后,考虑我们的范式著名麦克斯韦妖的悖论中的解决方案。让我提醒你,他如下。假设我们有蓝色和红色的分子的混合气体。把后面的分区,做小孔,降落在一个虚构的恶魔。他的任务 - 从左至右唯一的红色和蓝色仅传递从右到左。很明显,经过一段时间后的气体将被再次分为:所有蓝色分子将被留在壁的,并且所有的红 - 右
。
事实证明,我们的妖下降了系统的熵。与恶魔,什么都没有发生,那就是它的熵并没有改变,但是系统,我们已经关闭。事实证明,我们发现,其中热力学第二定律并不满足一个例子!因此是可能的吗?
我们解决这个矛盾,但是,是非常简单的。熵之后 - 这个属性是不系统,以及我们对系统的知识。我们都知道,系统一点点,所以我们认为它的熵减小。然而,我们的系统守护进程知道了很多 - 让不同的分子,它必须知道他们每个人的位置和速度(至少在其方法)。如果他知道一切关于分子,然后从他的角度来看,该系统的熵,其实是零 - 它没有关于它缺少的信息。在这种情况下,该系统的熵作为等于零,并保持在零,和热力学第二定律从不干扰。
但即使妖不知道所有关于系统的微观信息,它是,至少,有必要知道分子的颜色飞起来给他看她通过与否。如果分子总数等于N,守护程序应该有系统信息N位 - 这么多的信息,但我们失去了当打开隔。即,丢失的信息的数目正好等于信息被有关系统将其返回到其原始状态中获得的量 - 它听起来很合乎逻辑的,并且,再次,并不矛盾热力学第二定律。
来源: geektimes.ru/post/246406/
熵。也许这是最困难的理解的概念,通过它可以在物理的过程中满足,至少当它涉及到经典物理学之一。几个研究生,可以解释它是什么。大多数问题与熵的理解,但是,可以删除,如果明白了一件事。熵是从其他热力学量有质的不同:如压力,体积,或内部的能量,因为它不是系统的属性,以及我们如何看待这个系统。不幸的是,在热力学过程中它通常与其他热力学函数,这加剧了误解考虑。
那么,什么是熵?
简而言之,该
<大段引用>熵 - 这是如何了大量的信息,你不知道系统 BLOCKQUOTE>例如,如果你问我,我住的地方,我会回答:在俄罗斯,我的熵值高的你,毕竟,俄罗斯大国。如果我给你打电话我邮政编码:603081,我的熵为你减少,因为你会得到更多的信息
。

邮编包含六个数字,那就是,我已经给你的信息,六个字符。熵你对我的知识下降约6个字符。 (事实上,这是不是因为有些指标对应多个地址,以及一些 - 少了,但我们忽略了这些)
。

或考虑另一个例子。假设我有十个骰子(十六进制),并把他们的,我告诉你,他们的总和等于30。只知道,你不能说每个骨头什么具体的数字 - 你没有足够的信息。在统计物理上的骨头,这些具体的数字称为微观,以及(在本例中30)的总金额 - 宏观态。有对应于这样的宏观态的熵是约6,5个字符(一半来自事实的量等于30 2930455微观即微观的顺序编号在第七排你,不是所有的数字,但只有0, 1和2)。
而且如果我告诉你,和等于59?要做到这一点,也只有10宏观态可能微观,使得它的熵是只有一个字符。正如你所看到的,不同的宏观态有不同的熵。
现在让我告诉你,第一个五年骨头13的总和,总和其余五 - 17,使超过30你有总量,但是,在这种情况下,提供更多的信息,因此系统对您的熵应该下降。事实上,5骨头13可以接收420个不同的方式,和17 - 780次,显微镜化妆即总数系统的唯一420h780 327 = 600。约一个字符的熵是比在第一实施例小。
我们测量记录微观的数目所需的字符数的熵。在数学上,它被定义为数目的对数,所以表示熵S中的符号,而微观符号Ω的数量,我们可以写出:
S =日志Ω
这不过是波尔兹曼式(最多一个因子k,取决于测量的选择的单位),进行熵。如果宏观态符合一项微观状态,它的熵这个公式是零。如果你有两个系统,总熵等于每个系统的熵的总和,因为日志(AB)=登录A +登录B.

从上面的描述可以清楚为什么我们不应该认为熵作为系统的性能。该系统具有opedelёnnye内部的能量,动量,充电,但它没有具体的熵:熵10骨头取决于你只知道他们的全部金额,或也部分和五岁以下儿童的骨骼
。
换句话说,熵 - 这就是我们如何描述系统。这使得它更从中取得物理学工作的其他值不同。
实物例证:在活塞
气 经典系统,这被认为在物理,是包含在所述活塞下的容器中的气体。气微状态 - 这是位置和它的每一个分子的动量(速度)。这等同于说你知道落在每个骨的早期上面的例子中的值。宏观态气体被描述这样的量如压力,密度,体积,化学组合物。这是关于轧制骰子的值的总和。

量描述宏观态可以通过一个所谓的“状态方程”可以相互结合。这种连接的存在允许,不知道微观预测会发生什么我们的系统,如果你启动加热或移动的活塞。对于状态的理想气体状态方程具有形式简单:
P =ρT
虽然你可能更熟悉的克拉珀龙 - 门捷列夫PV =νRT - 这是相同的公式,但与另外一对常量来迷惑你。更多的微状态满足这一宏观态是更多的粒子是我们的制度更好地描述其状态方程的一部分。为气体的颗粒数的典型值是阿伏伽德罗数,即10个顺序 23 SUP>的。
量,如压力,温度和密度平均的称呼,是因为它们的平均,对应于给定宏观态(或相当接近它的宏观状态)持续连续微观状态。要找出哪些微观状态是一个系统,我们需要大量的信息 - 我们需要知道每个粒子的位置和速度。这个信息的量称为熵。
如何在宏观态的熵的变化?这是很容易理解的。例如,如果我们有一个小的热气体,其颗粒将增加的速度,因此,将增加,并且我们的无知有关速度的程度,即,熵增。或者,如果我们增加气体的体积通过推动活塞以增加我们的粒子的位置的无知的程度,和熵也将增长。
固体和势能
如果我们考虑一个气体代替的固体本体,特别是与一个有序结构作为晶体,例如,一个金属片,其熵小。怎么会?因为知道在该结构中,要知道,和所有其他的位置(它们被布置成规则的晶体结构)的单个原子的位置,原子的速度是小的,因为它们不能飞离它们的位置和仅轻微振荡围绕平衡位置。< BR />

如果一块金属是在重力场中(例如,地球的表面上方升高),在该金属的每个原子的势能近似等于其它原子的势能,以及与此相关的能量熵是低的。这不同于动能势能,这对于热运动可以从原子向原子而变化。
如果一个金属片,提升到一定高度,让他们去,其势能转换成动能,而是熵增加会有一点,因为所有的原子会移动近似相同。但是,当一个片落在地上的击期间金属原子将具有随机的方向,和熵显着增加。的定向运动的动能进入热运动的动能。之前我们打了一些知道如何将每个原子,现在我们已经失去了这一信息。
了解热力学第二定律
热力学第二定律指出熵(封闭系统)总是增加。现在我们可以理解为什么:因为你不能一下子获得有关微观的更多信息。一旦你失去了关于微状态的一些信息(如影响地面上的一块金属的过程中),你不能返回回来。

让我们回到骰子。回想一下,一共有59宏观态具有非常低的熵,同时也得到它不是那么简单。如果一次又一次掷骰子,它会掉出的量(宏观态),其对应于更多数量的微观的是要实现宏观态大熵。最大熵共有35人,她就会更经常比别人落下。仅此而已,说热力学第二定律。任何随机(不受控制)相互作用导致的增加的熵的,至少直到它到达它的最大值。
搅拌气体
并保证说一个例子。假设我们有一个容器,其中有两个气体分离位于容器壁的中间。我们称一个气体分子蓝,其他 - 红
如果打开隔板,气体开始搅拌,因为微观的数,其中混合气体比微状态中它们被分离大得多,而且微状态所有天然同等。当我们打开该分区的每个分子,我们失去了分区的哪个方面的信息,这就是现在。如果分子是N,信息的N个位丢失(在这种情况下的位或符号,它实际上是相同的,并且仅相差一些常数因子)。
研究了麦克斯韦妖
最后,考虑我们的范式著名麦克斯韦妖的悖论中的解决方案。让我提醒你,他如下。假设我们有蓝色和红色的分子的混合气体。把后面的分区,做小孔,降落在一个虚构的恶魔。他的任务 - 从左至右唯一的红色和蓝色仅传递从右到左。很明显,经过一段时间后的气体将被再次分为:所有蓝色分子将被留在壁的,并且所有的红 - 右
。

事实证明,我们的妖下降了系统的熵。与恶魔,什么都没有发生,那就是它的熵并没有改变,但是系统,我们已经关闭。事实证明,我们发现,其中热力学第二定律并不满足一个例子!因此是可能的吗?
我们解决这个矛盾,但是,是非常简单的。熵之后 - 这个属性是不系统,以及我们对系统的知识。我们都知道,系统一点点,所以我们认为它的熵减小。然而,我们的系统守护进程知道了很多 - 让不同的分子,它必须知道他们每个人的位置和速度(至少在其方法)。如果他知道一切关于分子,然后从他的角度来看,该系统的熵,其实是零 - 它没有关于它缺少的信息。在这种情况下,该系统的熵作为等于零,并保持在零,和热力学第二定律从不干扰。
但即使妖不知道所有关于系统的微观信息,它是,至少,有必要知道分子的颜色飞起来给他看她通过与否。如果分子总数等于N,守护程序应该有系统信息N位 - 这么多的信息,但我们失去了当打开隔。即,丢失的信息的数目正好等于信息被有关系统将其返回到其原始状态中获得的量 - 它听起来很合乎逻辑的,并且,再次,并不矛盾热力学第二定律。
来源: geektimes.ru/post/246406/