La entropía? ¡Es fácil! Bashny.Net

Este post es una traducción libre de la respuesta que Marcos Eichenlaub dio a la pregunta ¿Cuál es una forma intuitiva de entender la entropía? , dada en el sitio Quora i>

Entropía. Tal vez este es uno de los conceptos más difíciles de entender con la que puedes conocer en el curso de la física, al menos cuando se trata de la física clásica. Pocos graduado, se puede explicar lo que es. La mayoría de los problemas con la comprensión de la entropía, sin embargo, se puede quitar si que entender una cosa. La entropía es cualitativamente diferente de otras cantidades termodinámicas: como la presión, el volumen o la energía interna, porque no es una propiedad del sistema, y ​​cómo nos fijamos en este sistema. Por desgracia, en el curso de la termodinámica que se considera generalmente junto con otras funciones termodinámicas, lo que agrava el malentendido.




Entonces, ¿qué es la entropía?
En pocas palabras, la

La entropía - que es como una gran cantidad de información que usted no sabe acerca del sistema blockquote> Por ejemplo, si usted me pregunta donde vivo, y yo te responderé: en Rusia, mi entropía es alto para usted, después de todo, Rusia país grande. Si te llamo mi código postal: 603081, mi entropía disminuye para usted, porque obtendrá más información
.

Código postal contiene seis dígitos, es decir, que te he dado seis caracteres de información. Entropía su conocimiento de mí cayó aproximadamente 6 caracteres. (De hecho, no se debe a que algunos índices corresponden más direcciones, y algunos - menos, pero descuidamos la estos)
.

O consideremos otro ejemplo. Supongamos que tengo diez dados (hex), y los echan, te digo que su suma es igual a 30. Sabiendo sólo eso, no se puede decir lo que los números específicos en cada uno de los huesos - usted no tiene suficiente información. Estas cifras específicas sobre los huesos de la física estadística llamados microestados, y la cantidad total (30 en nuestro caso) - macroestado. Hay 2.930.455 microestados que corresponden a la cantidad igual a 30. Así que la entropía del macroestado es de unos 6, 5 caracteres (la mitad viene del hecho de que la numeración de microestados en orden en el séptimo de descarga que, no todos los números, pero sólo el 0, 1 y 2).

¿Y si te dijera que la suma es igual a 59? Para ello, sólo hay 10 macroestado microestados posibles, de modo que su entropía es sólo un carácter. Como se puede ver, diferente macroestado tienen diferentes entropía.

Ahora déjame decirte que la suma de los primeros cinco huesos 13, y la suma de los cinco restantes - 17, por lo que la cantidad total de más de 30. Usted tiene, sin embargo, en este caso, más información está disponible, por lo que la entropía del sistema para que usted debe caer. De hecho, cinco huesos 13 puede recibir 420-th maneras diferentes, y 17 a 780 °, es decir, el número total de maquillaje microscópica sólo 420h780 327 = 600. El entropía del sistema en aproximadamente un carácter es menor que en el primer ejemplo.

Medimos la entropía del número de caracteres necesarios para registrar el número de microestados. Matemáticamente, se define como el logaritmo del número, por lo que el símbolo que denota la entropía S, y el número de microestados símbolo Ω, podemos escribir:

S = log Ω

Esto no es más que la fórmula de Boltzmann (hasta un factor de k, que depende de la unidad de medida seleccionada) para la entropía. Si macroestado cumplen uno microestado, su entropía por esta fórmula es cero. Si dispone de dos sistemas, la entropía total es igual a la suma de la entropía de cada uno de estos sistemas, porque log (AB) = log A + log B.


De la descripción anterior se hace evidente por qué no debemos pensar en la entropía como propiedades del sistema. El sistema tiene opedelёnnye energía interna, el impulso, la carga, pero no tiene entropía específica: entropía diez huesos depende sólo conoce su importe total, o también las sumas parciales entre los cinco huesos
.
En otras palabras, la entropía - que es como se describe el sistema. Y eso lo hace muy diferente de otros valores que hicieron el trabajo en la física.

Ejemplo físico: gas bajo la
pistón Sistema clásico, que se considera en la física, es el gas contenido en el recipiente debajo del pistón. Microestado de gas - es la posición y el momento (velocidad) de cada una de sus moléculas. Esto es equivalente a decir que usted sabe el valor que cayó sobre cada hueso en el ejemplo anterior antes. Gas macroestado se describe cantidades tales que la presión, densidad, volumen, composición química. Esta es la suma de los valores en los dados laminados.


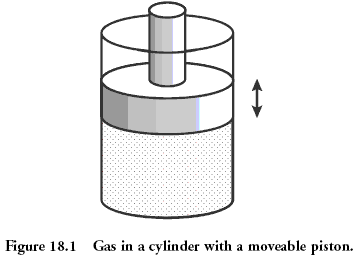
Las cantidades que describen macroestado pueden estar unidos entre sí a través de un llamado "ecuación de estado". La presencia de esta conexión permite, sin saber microestados de predecir lo que va a pasar con nuestro sistema, si usted comienza a fuentes de calor o para mover el pistón. Para una ecuación del gas ideal de estado tiene la forma simple:

p = ρT

aunque es probable que estar más familiarizado con el Clapeyron - Mendeleev pV = νRT - esta es la misma ecuación, pero con la adición de un par de constantes para confundirte. Los más microestados cumplen este macroestado que es más partículas son parte de nuestro sistema se describa mejor su ecuación de estado. Para los valores típicos de la cantidad de partículas de gas son el número de Avogadro, que es del orden de 10 <sup>23 sup>.

Cantidades tales como la presión, temperatura y densidad promediadas llamados porque se promedian para continuas microestados sucesivas correspondientes a un macroestado dado (o más bien cerca de ella macroestados). Para averiguar qué microestado es un sistema, necesitamos una gran cantidad de información - lo que necesitamos saber la posición y velocidad de cada partícula. El importe de esta información se denomina entropía.

¿Cómo funciona el cambio de entropía de un macroestado? Es fácil de entender. Por ejemplo, si tenemos un poco de calor del gas, la velocidad de sus partículas aumentará, por lo tanto, aumentará y la medida de nuestra ignorancia acerca de la velocidad, es decir, el aumento de entropía. O, si aumentamos el volumen de gas empujando el pistón para aumentar el alcance de nuestra ignorancia de las posiciones de las partículas, y la entropía también crecerá.

Sólidos y el potencial
energía Si consideramos un gas en lugar de un cuerpo sólido, en particular, con una estructura ordenada como un cristal, por ejemplo, una pieza de metal, su entropía es pequeña. Cómo? Debido a conocer la posición de un solo átomo en esta estructura, sabes, y la posición de todos los demás (que se disponen en una estructura cristalina regular), la velocidad de los átomos es pequeño, porque no pueden volar lejos de su posición y sólo ligeramente oscilar alrededor de la posición de equilibrio. < br />

Si una pieza de metal se encuentra en un campo gravitatorio (por ejemplo, elevada por encima de la superficie de la Tierra), la energía potencial de cada átomo en el metal es aproximadamente igual a la energía potencial de otros átomos, y se asocia con esta entropía de energía es bajo. Esto difiere de la energía potencial cinética, que para el movimiento térmico puede variar de átomo a átomo.

Si una pieza de metal, elevado a una cierta altura, que se vayan, su energía potencial se convierte en energía cinética, pero la entropía aumenta habrá poco, porque todos los átomos se moverán aproximadamente la misma. Pero cuando una pieza cae al suelo durante la huelga de los átomos del metal tendrán una dirección aleatoria, y la entropía aumentará dramáticamente. La energía cinética del movimiento dirigido entra en la energía cinética del movimiento térmico. Antes de llegar a algunas sabemos cómo mover cada átomo, ahora que hemos perdido esta información.

Comprender la segunda ley de la termodinámica
La segunda ley de la termodinámica dice que la entropía (sistema cerrado) siempre aumenta. Ahora podemos entender por qué: porque no se puede llegar de pronto más información sobre microestados. Tan pronto como se pierde alguna información acerca de microestado (como durante el impacto de un trozo de metal en el suelo), no se puede volver atrás.


Volvamos a los dados. Recordemos que macroestado con un total de 59 tiene una entropía muy baja, pero también entiendo que no es tan simple. Si tirar los dados una y otra vez, caerá fuera de la cantidades (macroestado), que corresponde a un mayor número de microestados que va a ser implementado macroestado con gran entropía. El mayor entropía tiene un total de 35, y que ella va a caer con más frecuencia que otros. Eso es todo, y dicha segunda ley de la termodinámica. Cualquier (no controlada) la interacción aleatoria conduce a un aumento en la entropía, al menos hasta que alcance su máximo.

Revolviendo
gas Y un ejemplo más para asegurar dijo. Supongamos que tenemos un contenedor en el que hay dos gas separado situado en el medio de la pared del recipiente. Llamamos a una molécula de gas de color azul, y el otro -. Rojo

Si el mamparo abierto, los gases empiezan a moverse, porque el número de microscópica donde los gases mezclados es mucho mayor que Microstates en el que se separaron, y microestado todo naturalmente igual. Cuando abrimos la partición para cada molécula perdimos información de qué lado de la partición, que es ahora. Si las moléculas son N, los N bits de información se pierde (bits o símbolos en este contexto, en realidad es el mismo, y sólo se diferencian por un factor constante).

Investigado con demonio
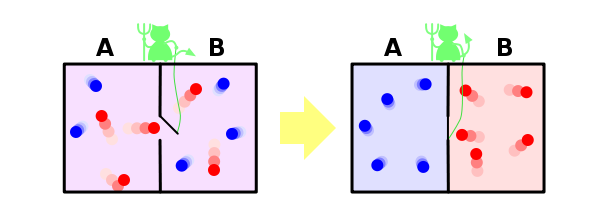
de Maxwell Y, por último, considere la solución dentro de nuestro paradigma famosa paradoja del demonio de Maxwell. Permítanme que les recuerde que él es el siguiente. Supongamos que tenemos una mezcla de gases de moléculas de color azul y rojo. Poner de nuevo la partición y hacer el agujero pequeño, que aterrizó en un demonio imaginario. Su tarea - para pasar de izquierda a derecha en rojo y azul sólo de derecha a izquierda. Es obvio que después de algún tiempo los gases se dividirán de nuevo: todas las moléculas azules serán dejadas de las paredes, y todo el rojo - derecha
.

Resulta que nuestro demonio dejó caer la entropía del sistema. Con el demonio, no pasó nada, es decir, su entropía no ha cambiado, pero el sistema que había cerrado. Resulta que encontramos un ejemplo en la segunda ley de la termodinámica no es satisfecha! Como tal fue posible?

Resolvemos esta paradoja, sin embargo, es muy simple. Después de la entropía - esta propiedad no es el sistema, y ​​nuestro conocimiento sobre el sistema. Todos sabemos sobre el sistema un poco, ¿por qué pensamos que su entropía disminuye. Sin embargo, nuestro demonio del sistema sabe mucho - por lo que las moléculas separadas, debe conocer la posición y velocidad de cada uno de ellos (al menos en la aproximación a la misma). Si él lo sabe todo sobre las moléculas, entonces, desde su punto de vista, la entropía del sistema, de hecho, es cero - que no tiene la información que falta en ello. En este caso, la entropía del sistema como igual a cero y permanece en cero, y la segunda ley de la termodinámica no es perturbado.

Pero incluso si el demonio no conoce toda la información sobre el microestado del sistema, es, al menos, es necesario conocer el color de la molécula vuela hacia él al verla pasar o no. Si el número total de moléculas es igual a N, el demonio debe tener N bits de información del sistema - tanto la información, sino que perdió cuando se abre el tabique. Es decir, el número de información perdida es exactamente igual a la cantidad de información que se obtenga sobre el sistema para devolverlo a su estado original - y suena bastante lógico, y, de nuevo, no contradice la segunda ley de la termodinámica.

Fuente: geektimes.ru/post/246406/</sup>