The shape of the universe: a lot of opportunities, but the reality is one

Do not erase the past. It shapes you today and helps you become who you will be tomorrow.

Ziad K. Abdelnuar blockquote>
 The universe even more than we are, to create the conditions that existed at the time of her birth. But what form it took? I chose to question the reader Tom Berry, who asks:

I understand that the universe form the seat. I wonder why the Big Bang, all matter is not scattered uniformly in all directions and has not given a spherical shape of the universe? Blockquote>
 Let's start with the fact that uberёm one dimension, and talk about what constitutes a two-dimensional surface. You probably imagine a plane - like a sheet of paper. It can be rolled into a cylinder and at the surface would be self-bonded - on the one hand, you can go to the other, it will still be a flat surface.

What does it mean? For example, you can draw a triangle and fold the size of inner corners. If we get 180 degrees, the surface - flat. If you draw two parallel lines, they will remain the same all along.

But this is only one option.



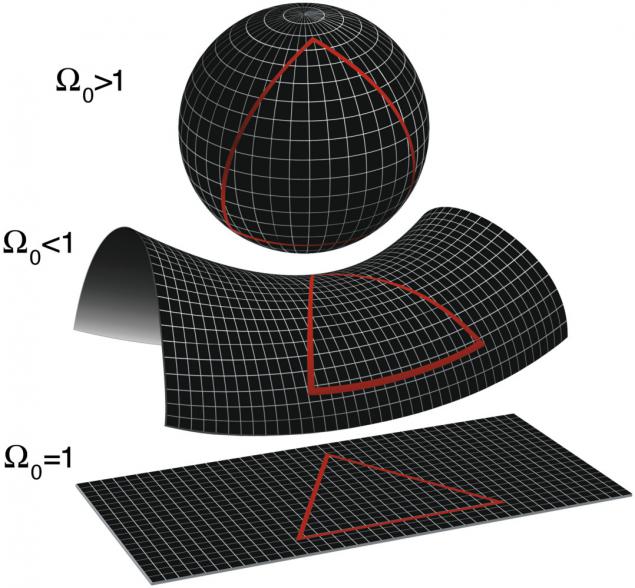
The surface areas - two-dimensional, but not flat. Any line starts to wrap, and if you add up the angles of the triangle, you get a value of more than 180 degrees. Drawing a parallel lines (lines that begin like parallel), you will see that, in the end, they meet and intersect. Such surfaces have positive curvature.

The surface of the seat, on the other hand, represents another type of two-dimensional non-planar surface. It is concave in one direction and convex on the other, perpendicular to, and is a surface with negative curvature. If you draw a triangle on it, you will get less than the sum of the angles of 180 degrees. Two parallel lines will diverge in different directions.



You can still submit a flat circular piece of paper. If you cut out a wedge and re-glue it, you will get a surface of positive curvature. If you insert this wedge in another piece of the same, you get the surface of negative curvature, as in the picture.

Two-dimensional surface is quite simple to imagine from the three-dimensional space. But in our three-dimensional universe things are little more complicated.



As to the curvature of the universe, we have three options:

- Positive curvature, like the scope of the higher dimensions
- Negative, as if the seat in the higher dimensions
- Zero (flat) - as a three-dimensional lattice

One would think that the existence of the Big Bang suggests the first spherical option because the universe seems to be the same in all directions - but it's not. There is a very interesting reason why the universe is the same in all directions - and it has nothing to do with the curvature.



The fact that the universe is the same in all places (homogeneous) and directions (isotropic), proves the existence of the Big Bang hypothesis which says that it all started with the hot and dense homogeneous state in which the initial conditions and the laws of nature are the same everywhere.

Over time, small deviations lead to the appearance of structures - stars, galaxies, clusters, and great voids. But the reason for the uniformity of the universe - that all had the same beginning, not in the curvature.

But we can measure the amount of curvature.



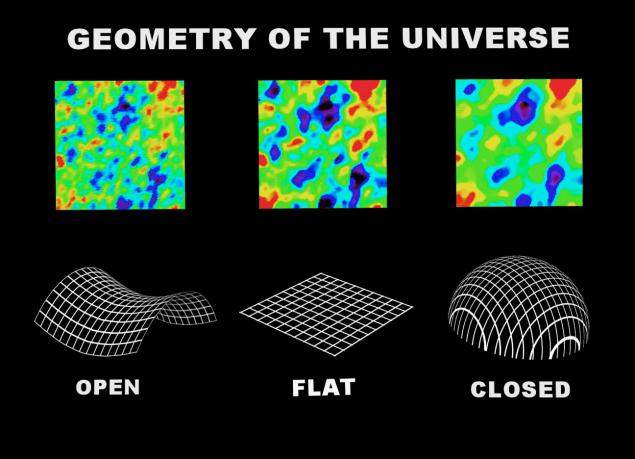
The picture presented fluctuation patterns imprinted in the CMB. From the way the universe works and what it consists of, peaks depend on fluctuations - the hottest and coldest places on the specific angular scales. If the negative curvature of the universe (saddle), the universe tends to a smaller scale, if positive - for more.

The same reason that we have described - as straight lines behave on these surfaces.



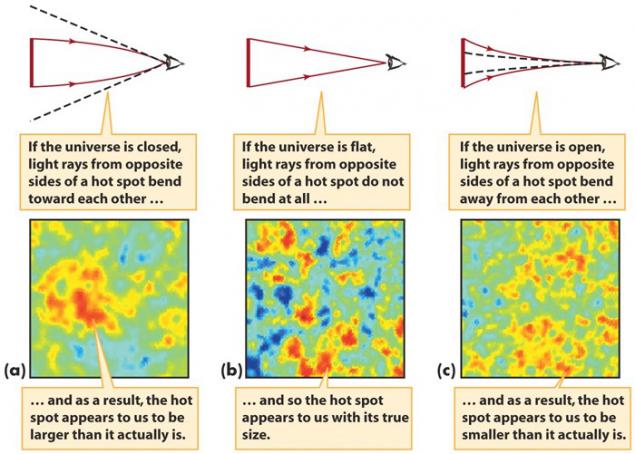
So we just need to study fluctuations in the cosmic microwave background radiation, and we can measure the curvature of the observable universe.

And what do we get?



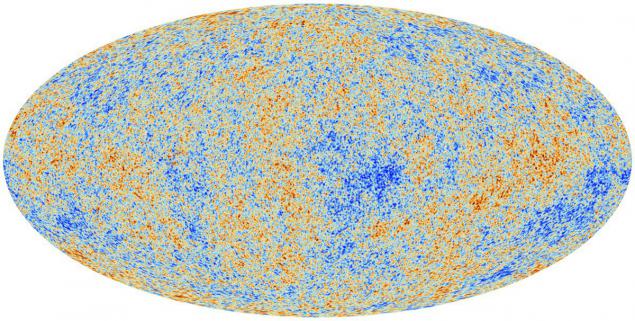
And we get that the value of the curvature shown circled in blue, equal to about 0.5%. This suggests that the curvature of the universe is indistinguishable from the plane.

She really expanding uniformly in all directions, but the curvature is not relevant. Of course, much more than we can see the scale of the curvature of the universe can be non-zero. The inflationary process takes place after the Big Bang, exponentially increases every part of the universe.



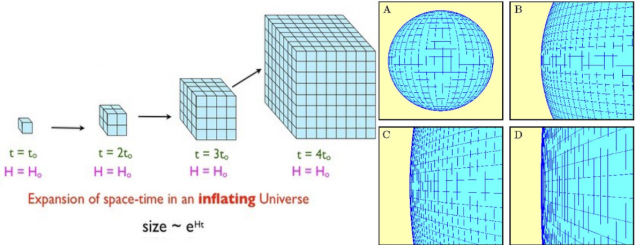
That is, it is possible that the curvature of the universe, positive or negative, that it looks like a saddle or a sphere, it can be self-bonded, and we will be able to go from one end and get to another. It can not be excluded - but the observable part of it is not. And for us the universe is indistinguishable from a plane. But, as shown in Part D, you can assume that your space is flat, and thus the universe can not be flat. This is the conclusion from the information we have.

Source: geektimes.ru/post/250160/