613
0.1
2016-09-20
10 измерений реальности: просто и понятно о теории струн
Считаем от трёх до десяти
Самая большая проблема у теоретических физиков — как объединить все фундаментальные взаимодействия (гравитационное, электромагнитное, слабое и сильное) в единую теорию. Теория суперструн как раз претендует на роль Теории Всего.Но оказалось, что самое удобное количество измерений, необходимое для работы этой теории — целых десять (девять из которых — пространственные, и одно — временное)! Если измерений больше или меньше, математические уравнения дают иррациональные результаты, уходящие в бесконечность — сингулярность.
Следующий этап развития теории суперструн — М-теория — насчитала уже одиннадцать размерностей. А ещё один её вариант — F-теория — все двенадцать. И это вовсе не усложнение. F-теория описывает 12-мерное пространство более простыми уравнениями, чем М-теория — 11-мерное.

Конечно, теоретическая физика не зря называется теоретической. Все её достижения существуют пока что только на бумаге. Так, чтобы объяснить почему же мы можем перемещаться только в трёхмерном пространстве, учёные заговорили о том, как несчастным остальным измерениям пришлось скукожиться в компактные сферы на квантовом уровне. Если быть точными, то не в сферы, а в пространства Калаби-Яу. Это такие трёхмерные фигурки, внутри которых свой собственный мир с собственной размерностью. Двухмерная проекция подобный многообразий выглядит приблизительно так:

Таких фигурок известно более 470 миллионов. Которая из них соответствует нашей действительности, в данный момент вычисляется. Нелегко это — быть теоретическим физиком.
Да, это кажется немного притянутым за уши. Но может, именно этим и объясняется, почему квантовый мир так отличается от воспринимаемого нами.
Точка, точка, запятая
Начнём с начала. Нулевое измерение — это точка. У неё нет размеров. Двигаться некуда, никаких координат для обозначения местонахождения в таком измерении не нужно.Поставим рядом с первой точкой вторую и проведём через них линию. Вот вам и первое измерение. У одномерного объекта есть размер — длина, но нет ни ширины, ни глубины. Движение в рамках одномерного пространства очень ограничено, ведь возникшее на пути препятствие не обойдёшь. Чтобы определить местонахождение на этом отрезке, понадобится всего одна координата.
Поставим рядом с отрезком точку. Чтобы уместить оба эти объекта, нам потребуется уже двумерное пространство, обладающее длиной и шириной, то есть, площадью, однако без глубины, то есть, объёма. Расположение любой точки на этом поле определяется двумя координатами.
Третье измерение возникает, когда мы добавляем к этой система третью ось координат. Нам, жителям трёхмерной вселенной, очень легко это представить.
Попробуем вообразить, как видят мир жители двухмерного пространства. Например, вот эти два человечка:

Каждый из них увидит своего товарища вот таким:

А при вот таком раскладе:
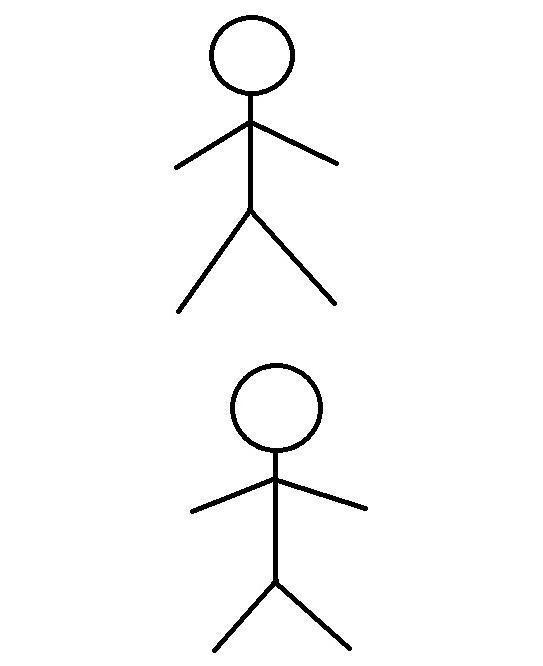
Наши герои увидят друг друга такими:

Именно смена точки обзора позволяет нашим героям судить друг о друге как о двумерных объектах, а не одномерных отрезках.
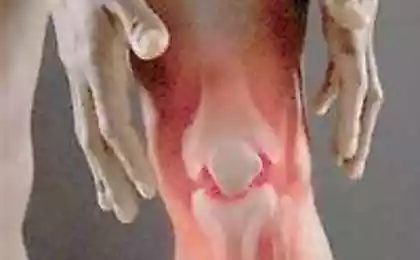
А теперь представим, что некий объёмный объект движется в третьем измерении, которое пересекает этот двумерный мир. Для стороннего наблюдателя, это движение выразится в смене двумерных проекций объекта на плоскости, как у брокколи в аппарате МРТ:
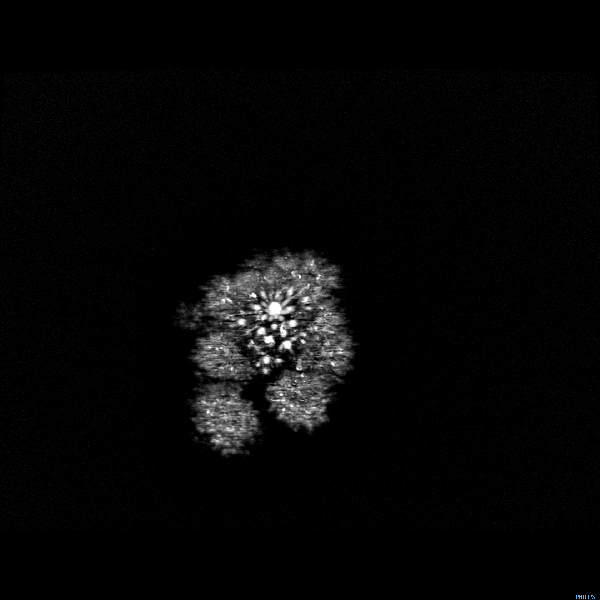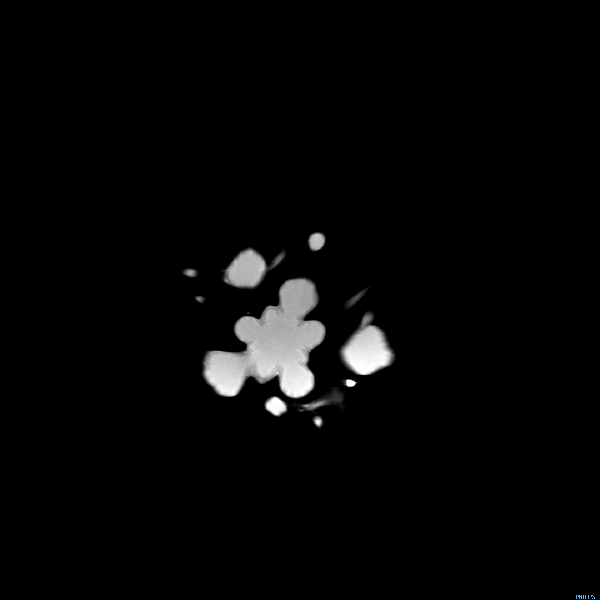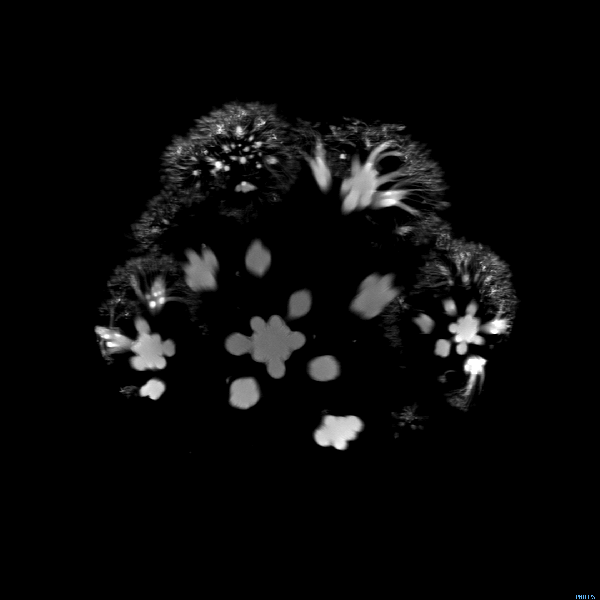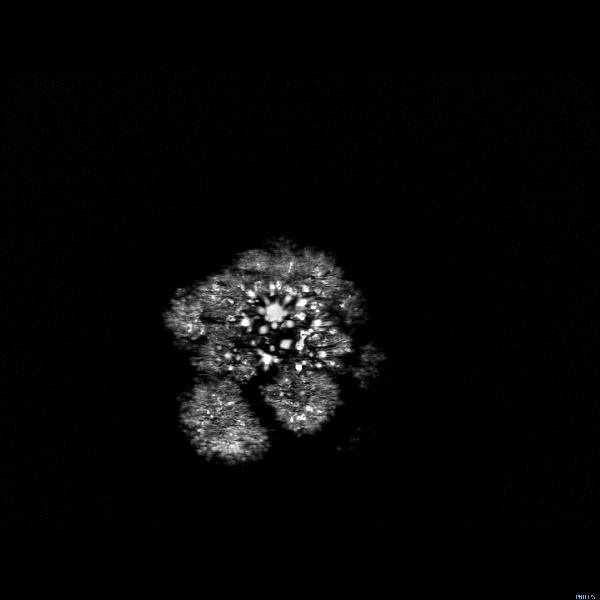
Но для обитателя нашей Флатландии такая картинка непостижима! Он не в состоянии даже представить её себе. Для него каждая из двумерных проекций будет видеться одномерным отрезком с загадочно переменчивой длиной, возникающим в непредсказуемом месте и также непредсказуемо исчезающим. Попытки просчитать длину и место возникновения таких объектов с помощью законов физики двумерного пространства, обречены на провал.
Мы, обитатели трёхмерного мира, видим всё двумерным. Только перемещение предмета в пространстве позволяет нам почувствовать его объём. Любой многомерный объект мы увидим также двумерным, но он будет удивительным образом меняться в зависимости от нашего с ним взаиморасположения или времени.
С этой точки зрения интересно думать, например, про гравитацию. Все, наверное, видели, подобные картинки:

На них принято изображать, как гравитация искривляет пространство-время. Искривляет… куда? Точно ни в одно из знакомых нам измерений. А квантовое туннелирование, то есть, способность частицы исчезать в одном месте и появляться совсем в другом, причём за препятствием, сквозь которое в наших реалиях она не смогла бы проникнуть, не проделав в нём дыру? А чёрные дыры? А что, если все эти и другие загадки современной науки объясняются тем, что геометрия пространства совсем не такая, какой мы привыкли её воспринимать?
Тикают часики
Время добавляет к нашей Вселенной ещё одну координату. Для того, чтобы вечеринка состоялась, нужно знать не только в каком баре она произойдёт, но и точное время этого события.Исходя из нашего восприятия, время — это не столько прямая, как луч. То есть, у него есть отправная точка, а движение осуществляется только в одном направлении — из прошлого в будущее. Причём реально только настоящее. Ни прошлое, ни будущее не существуют, как не существуют завтраки и ужины с точки зрения офисного клерка в обеденный перерыв.
Но теория относительности с этим не согласна. С её точки зрения, время — это полноценное измерение. Все события, которые существовали, существуют и будут существовать, одинаково реальны, как реален морской пляж, независимо от того, где именно мечты о шуме прибоя захватили нас врасплох. Наше восприятие — это всего лишь что-то вроде прожектора, который освещает на прямой времени какой-то отрезок. Человечество в его четвёртом измерении выглядит приблизительно так:

Но мы видим только проекцию, срез этого измерения в каждый отдельный момент времени. Да-да, как брокколи в аппарате МРТ.
До сих пор все теории работали с большим количеством пространственных измерений, а временное всегда было единственным. Но почему пространство допускает появление множественных размерностей для пространства, но время только одно? Пока учёные не смогут ответить на этот вопрос, гипотеза о двух или более временных пространствах будет казаться очень привлекательной всем философам и фантастам. Да и физикам, чего уж там. Скажем, американский астрофизик Ицхак Барс корнем всех бед с Теорией Всего видит как раз упущенное из виду второе временное измерение. В качестве умственного упражнения, попробуем представить себе мир с двумя временами.
Каждое измерение существует отдельно. Это выражается в том, что если мы меняем координаты объекта в одной размерности, координаты в других могут оставаться неизменными. Так, если вы движетесь по одной временной оси, которая пересекает другую под прямым углом, то в точке пересечения время вокруг остановится. На практике это будет выглядеть приблизительно так:

Всё, что Нео нужно было сделать — это разместить свою одномерную временную ось перпендикулярно временной оси пуль. Сущий пустяк, согласитесь. На самом деле всё намного сложнее.
Точное время во вселенной с двумя временными измерениями будет определяться двумя значениями. Слабо представить себе двумерное событие? То есть, такое, которое протяжённо одновременно по двум временным осям? Вполне вероятно, что в таком мире потребуются специалисты по составлению карты времени, как картографы составляют карты двухмерной поверхности земного шара.
Что ещё отличает двумерное пространство от одномерного? Возможность обходить препятствие, например. Это уже совсем за границами нашего разума. Житель одномерного мира не может представить себе как это — завернуть за угол. Да и что это такое — угол во времени? Кроме того, в двумерном пространстве можно путешествовать вперёд, назад, да хоть по диагонали. Я без понятия как это — пройти через время по диагонали. Я уж не говорю о том, что время лежит в основе многих физических законов, и как изменится физика Вселенной с появлением ещё одного временного измерения, невозможно представить. Но размышлять об этом так увлекательно!
Очень большая энциклопедия
Другие измерения ещё не открыты, и существуют только в математических моделях. Но можно попробовать представить их так.Как мы выяснили раньше, мы видим трёхмерную проекцию четвёртого (временного) измерения Вселенной. Другими словами, каждый момент существования нашего мира — это точка (аналогично нулевому измерению) на отрезке времени от Большого взрыва до Конца Света.
Те из вас, кто читал про перемещения во времени, знают какую важную роль в них играет искривление пространственно-временного континуума. Вот это и есть пятое измерение — именно в нём «сгибается» четырёхмерное пространство-время, чтобы сблизить две какие-то точки на этой прямой. Без этого путешествие между этими точками было бы слишком длительным, или вообще невозможным. Грубо говоря, пятое измерение аналогично второму — оно перемещает «одномерную» линию пространства-времени в «двумерную» плоскость со всеми вытекающими в виде возможности завернуть за угол.
Наши особо философско-настроенные читатели чуть ранее, наверное, задумались о возможности свободной воли в условиях, где будущее уже существует, но пока ещё не известно. Наука на этот вопрос отвечает так: вероятности. Будущее — это не палка, а целый веник из возможных вариантов развития событий. Какой из них осуществится — узнаем когда доберёмся.
Каждая из вероятностей существует в виде «одномерного» отрезка на «плоскости» пятого измерения. Как быстрее всего перескочить из одного отрезка на другой? Правильно — согнуть эту плоскость, как лист бумаги. Куда согнуть? И снова правильно — в шестом измерении, которое придаёт всей этой сложной структуре «объём». И, таким образом, делает её, подобно трёхмерному пространству, «законченной», новой точкой.
Седьмое измерение — это новая прямая, которая состоит из шестимерных «точек». Что представляет собой какая-либо другая точка на этой прямой? Весь бесконечный набор вариантов развития событий в другой вселенной, образованной не в результате Большого Взрыва, а в других условиях, и действующей по другим законам. То есть, седьмое измерение — это бусы из параллельных миров. Восьмое измерение собирает эти «прямые» в одну «плоскость». А девятое можно сравнить с книгой, которая уместила в себя все «листы» восьмого измерения. Это совокупность всех историй всех вселенных со всеми законами физики и всеми начальными условиями. Снова точка.
Тут мы упираемся в предел. Чтобы представить себе десятое измерение, нам нужна прямая. А какая может быть другая точка на этой прямой, если девятое измерение уже покрывает всё, что только можно себе представить, и даже то, что и представить невозможно? Получается, девятое измерение — это не очередная отправная точка, а финальная — для нашей фантазии, во всяком случае.
Теория струн утверждает, что именно в десятом измерении совершают свои колебания струны — базовые частицы, из которых состоит всё. Если десятое измерение содержит себе все вселенные и все возможности, то струны существуют везде и всё время. В смысле, каждая струна существует и в нашей вселенной, и любой другой. В любой момент времени. Сразу. Круто, да? опубликовано
P.S. И помните, всего лишь изменяя свое потребление — мы вместе изменяем мир! ©
Источник: revolverlab.com/10-izmereniy-realnosti-prosto-i-ponyatno-o-teorii-strun/
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.
3 самых страшных слова — обязанности, долг, ответственность
Необычный гараж Cardok — идеальное решение для небольшого участка